自古以来，程序员就以三高闻名于相亲市场，广受丈母娘欢迎。

哪三高？收入高、截留率高、死亡率高。

此话怎讲？

快二十年前程序员的月工资就可以过万，这在当时是一个很了不起的数目。即便是遍地程序员的今天，在牛马当中程序员的工资也是数一数二的，尤其是会做AI、懂ML的程序员。

大部分程序员没有什么奢侈的爱好，除了加班就是联网打打 Dota，花不了几个钱，剩下的都交给老婆。

因为精神压力大，程序员中年秃顶是标配，过劳死屡见不鲜，方便老婆带着存款开启人生第二春。

要是《白鹿原》写的是 IT 界，开篇应该是这样的：

“田小娥后来引以为豪壮的是一生里嫁过七个程序员。”

当然以上是程序员在自黑。程序员可能是历史上最喜欢自黑的群体。比如他们有这么一个段子：世界上有两种科学，一种是科学，另一种是计算机科学。

大家嘿嘿一笑之余，不要忘了这只是一个段子。计算机科学可不光可以帮你写个抢票网站，堆个小游戏。它也和其它自然科学一样博大精深。

作为数学的一个分支，计算机科学凝聚了无数先贤的智慧，有很多精妙绝伦美轮美奂，让人赞不绝口惊为天人的设计和思想。今天我就来讲一讲密码学中让我惊艳的一个算法：迪菲-赫尔曼（Diffie-Hellman）密钥交换算法。

～～～～

大家可能注意到，有的网站网址是http开头的，有的是https。有没有这个 s 有什么区别呢？

这里的 s 是 secure（安全）的意思。有小s，表示你的机器跟这个服务器之间的通信是安全的，不怕旁人偷听。比如说你在这个网站上填自己的身份信息，用 https 方式传送旁人就看不见你填的是啥。

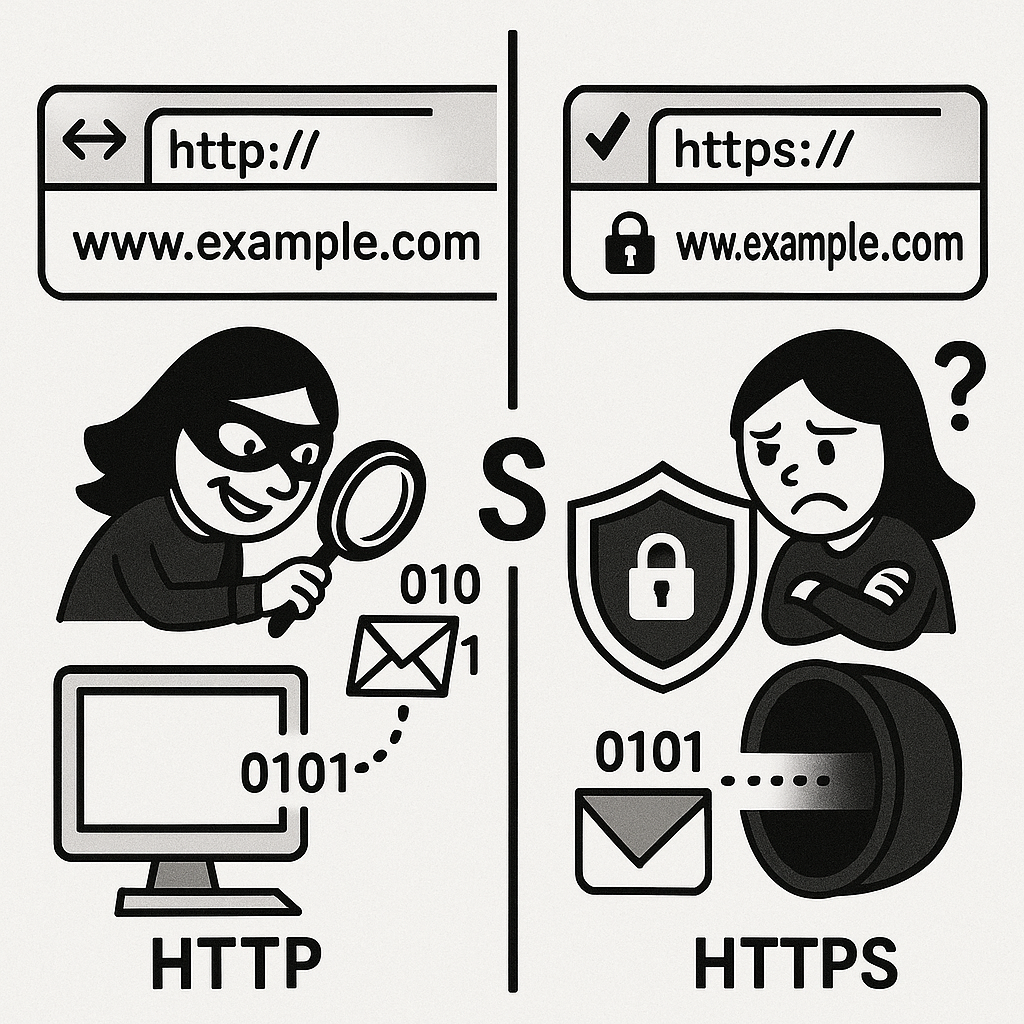
你有没有想过这是怎么做到的？

还能怎样？加密呗。

很好。那你有没有想过是用什么密钥加密的呢？

你连上这个网站的时候，系统并没有咨询过你“尊敬的客户，请问我们接下来的私密对话该用什么密钥？”所以这个密钥肯定不是你选的。

也不是你的浏览器替你选的。要是浏览器选了一个密钥 k 然后告诉网站“接下来咱俩的通信用 k 加密吧”，坏人偷听到这条消息不就可以冒充你或者网站了吗？

同样，也不可能是网站选的。

更不可能是在浏览器和网站的代码里事先固定的。这样很多人都有机会知道这个密钥，毫无安全可言。

所以，为了安全起见，https 协议要在每次建立一个新连接前，让浏览器和网站通过不安全的信道商量出一个秘密，而这个秘密只有它们双方知道，其他任何人都不知道 -- 哪怕他们偷听了全部商量过程。

等等！阳光之下没有秘密。这怎么可能？

迪菲-赫尔曼（Diffie-Hellman）算法就可以完成这个貌似不可能的任务。

在计算机密码学研究中，为了生动起见，经常把交互的双方叫做爱丽丝（Alice）和鲍勃（Bob）。这种做法相当于在中文中把丫鬟甲和宋兵乙换成李嘉欣和周星驰，可以让正在读文的同学虎躯一震，走出半梦半醒。

据说，这一招是发明 RSA 加密算法的三巨头想出来的。

不得不说这些大佬是懂营销的。搁在今天，绝对是百万大V。

好了，我们就借用爱丽丝和鲍勃来讲这个故事。因为待会儿要出现公式，为了预防读者划走，我特地引入了三角恋和暴力，还在文末留了两个八卦，请大家别走，坚持看完！

爱丽丝和鲍勃是一对高中生情侣，他们彼此爱你在心口难开。难开口是因为隔墙有耳，这个耳就是爱丽丝的情敌伊芙（Eve）。

顺便讲一句，在密码学研究中，偷听者这个角色通常是由伊芙扮演的，因为 Eve 和偷听（eavesdropper）谐音。

想不到啊想不到，浓眉大眼的计算机科学家也喜欢谐音梗。

这个伊芙不但是个恋爱脑，而且天赋异禀，爱丽丝和鲍勃的任何对话她都有办法听到。要是这两人的情话有啥地方刺激到了她，保不齐她一时冲动就让爱丽丝血溅当场。

爱丽丝的高中计算机课的老师迈克尔看在眼里，疼在心里，于是给大家加了一堂计算机密码学课程，让爱丽丝鲍勃茅塞顿开，从此可以不惧伊芙，在光天化日之下聊骚。

这是怎么做到的呢？

在下面的解说中，公开的消息用蓝字表示，未公开的秘密则用红字。

首先爱丽丝和鲍勃选了一个很大的，有几百位的素数 p，又随便选了一个也很大的正整数 g。整个过程都广而告之，所以我们可以假定伊芙对这两个数也是心知肚明。

然后，爱丽丝选了一个秘密正整数 a，这秘密埋藏在她心里，谁都不告诉。连鲍勃都不知道这个数，伊芙自然也不知道。

同样，鲍勃也想了一个秘密正整数 b，这个秘密他也守口如瓶。

然后他们各自做了一个计算，然后公布了计算结果。

爱丽丝算的是 p ^ a mod g（p 的 a 次方除以 g 的余数）。我们把它叫 m。

鲍勃算的是 p ^ b mod g（p 的 b 次方除以 g 的余数）。我们不妨叫它 n。

既然 m 和 n 是公开的，伊芙自然也知道咯。

爱丽丝和鲍勃看到对方的结果后，相视一笑，又做了第二步计算。

爱丽丝算的是 n ^ a mod g。我们把这个结果叫 s。

爱丽丝把 s 当成秘密，不告诉任何人。虽然伊芙知道 n 和 g，但她不知道 a，所以她算不出来 s 是多少。

鲍勃算的是 m ^ b mod g。结果也叫 s。鲍勃也把 s 当成秘密。

等等！咋能把两个数都叫 s 呢？这不搞混了吗？这不像正经科学家干的事啊。

这就是迪菲-赫尔曼算法的高光时刻。

原来，我们可以证明，爱丽丝算出来的 s 跟鲍勃算出来的 s 是一样的，所以把它们叫一个名字没有任何毛病。

证明过程用到了高等高中数学，我把它写在下面，供学有余力的朋友验证。没有兴趣的读者么，现在就可以跳到结尾看八卦去了。

爱丽丝算的是 n ^ a mod g = (p ^ b mod g) ^ a mod g = (p ^ b) ^ a mod g = p ^ (b×a) mod g

也就是 p 的 b×a 次方除以 g 的余数。

鲍勃算的是 m ^ b mod g = (p ^ a mod g) ^ b mod g = (p ^ a) ^ b mod g = p ^ (a×b) mod g

也就是 p 的 a×b 次方除以 g 的余数。

咦，b×a 跟 a×b 不是一样的么？所以他们算出来的这两个数原来是一样的。

现在，爱丽丝和鲍勃有了共同的秘密 s，就可以用 s 做密钥给他们的通信加密解密了。伊芙就算是看到全部通信内容，因为不知道密钥，也只能干瞪眼。

聪明的朋友会想到：伊芙虽然不知道 s 是多少，但她知道 p，g，m 和 n 啊！有了这四个数，她就不能推算出 s 来吗？

比如，她知道 m = p ^ a mod g，难道不能从 m，p 和 g 反推出 a？有了 a，不就可以算出 s 了？

还真不能。从 p，g 和 a 算 m 容易，从 p，g 和 m 算 a 是一个很难很难的问题，叫离散对数。算这东西可就要了亲命了，用最快的计算机也要 1000000…000 年，基本上那时候也不会有地球了。

这个精妙的算法依靠的是一种计算机科学中叫做单向函数的东西。顾名思义，单向函数就是从输入算输出容易，但是反过来从输出倒推输入非常困难的函数。比如说很多我们常用的哈希函数就是这样。还有大家熟知的大素数乘积的因子分解问题：如果 p 和 q 是两个很大的素数，k = p×q 很容易计算，但是反过来要把 k 拆成 p×q 可就难多了。这就是今天广泛应用的 RSA 非对称加密算法的基石。

～～～～

感谢大家读到这里。现在履行承诺，开始八卦。

我在美国读博的时候，选了一门密码学和安全的课程。讲课的教授在这个领域颇有些名气，叫迈克尔·费舍尔（Michael Fischer）。费教授是个满脸大胡子的美国白人老头，学问很好，但是讲课嘛，稍微有欠生动。而且他鼻音很重，对刚到美国的我是一个巨大的听力考验，所以这门课很多时候我都是靠看书自学的，因为跟上他的讲座对我来说非常困难。

从朋友那里我了解到费教授的太太叫爱丽丝，在附近的另一所大学做计算机系的主任。他俩还有一个儿子叫鲍勃，跟我在哈佛的一个大学同学是朋友。这些背景知识给我理解费舍尔教授讲课造成了很大的困扰。因为，我会自动脑补把费教授讲的爱丽丝替换成“我老婆”，把他讲的鲍勃换成“我儿子”。于是，在我听来，他讲的就是“我老婆给我儿子发了一条明文消息，被一个中间人截获了”。很快我就因为关心他家人的安危走神了。

学完这门课之后有一年，系里另一位博士生做开题报告，给大家介绍他接下来博士论文会做哪个方向。这位同学志向高远，要设计一个全新的选举制度。按照他的想法，这个制度有很多美好的特性，比如可以保障每个投票人不受人胁迫，也就是说如果有人拿着枪逼迫你投民主党，你可以糊弄他，嘴上说好，手上悄悄投共和党。

与此同时，在这位博士生同学的设想中，这个制度还能保证公正透明，就是说每个选民都可以去验证系统确实尊重了他的选择，不会出现他选的是民主党而系统把票记到共和党名下的情况。

听到这里，我感觉智力不够用了，于是举手提问：这两点不会互相矛盾吗？要是有办法验证系统记的票和我选的一致，那么也可能有人拿枪逼我验证我投的确实是民主党，不是就崩了我。一想到这个，我在当初投票时不就不敢投共和党了吗？我不就还是受到了胁迫吗？

那位同学听了我的质疑，沉默了两秒，然后讲了一大通话，有很多我不懂的术语。

我不是专业搞密码的，所以默默忍下了。

报告结束大家纷纷离场的时候，费舍尔教授向我走过来，对我说：刚才你说的那个问题，我认为你完全正确。

～～～～～～～～～～